Chapter 5 Derivation of Jarzynski Equality

Click Start Over at the left bottom to start Back to Contents

1 Jacobian determinant

Given two vectors $\overrightarrow{\alpha} = (\alpha_1, \alpha_2)$ and $\overrightarrow{\beta} = (\beta_1, \beta_2)$ as shown in Figure 1. The area of the parallelogram $dA$ can be calculated as

$dA = |\overrightarrow{\beta}|\cdot |\overrightarrow{\alpha}| \sin \theta = \alpha_1 \beta_2 - \alpha_2 \beta_1$

$\begin{equation} dA = |\overrightarrow{\alpha} \times \overrightarrow{\beta}| = \begin{vmatrix} \alpha_1 & \alpha_2 \\ \beta_1 & \beta_2 \end{vmatrix} \label{eq:cross-area} \end{equation}$

For an irregular infinitesimal area, the slope directions at the start point are chosen to represent the parallelogram sides.

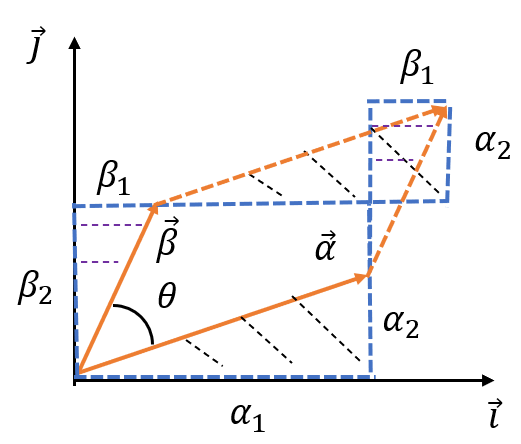
Figure 1: Relation between area of a parallelogram and cross product of two vectors.

Suppose that there exists a bijective transformation $T: u=u(x,y), v=v(x,y)$ mapping the rectangular area in the $xy$ plane to a parallelogram in the $uv$ plane as shown in Figure 2. Since

$du = u_x dx + u_y dy \\ dv = v_x dx + v_y dy$

or in maxtrix form

$\begin{bmatrix} du \\ dv \end{bmatrix} =\begin{bmatrix} u_x & u_y \\ v_x & v_y \end{bmatrix} \begin{bmatrix} dx \\ dy \end{bmatrix},$

the vectors $\overrightarrow{dx}=(dx, 0)$ and $\overrightarrow{dy}=(dy, 0)$ are transformed to $\overrightarrow{du}$ and $\overrightarrow{dv}$ as

$\overrightarrow{du} =\begin{bmatrix} u_x & u_y \\ v_x & v_y \end{bmatrix} \begin{bmatrix} dx \\ 0 \end{bmatrix} = \begin{bmatrix} u_x dx \\ v_x dx \end{bmatrix}$

and

$\overrightarrow{dv} =\begin{bmatrix} u_x & u_y \\ v_x & v_y \end{bmatrix} \begin{bmatrix} 0 \\ dy \end{bmatrix} = \begin{bmatrix} u_y dy \\ v_y dy \end{bmatrix}$

Using equation ( $\ref{eq:cross-area}$ ), we obtain the new area as

$\begin{equation} dA_{uv} = |\overrightarrow{du} \times \overrightarrow{dv}| = \left | \begin{bmatrix} u_x dx \\ v_x dx \end{bmatrix} \times \begin{bmatrix} u_y dy \\ v_y dy \end{bmatrix} \right | = |J| dx dy \label{eq:new.area} \end{equation}$

where $J = \left| \frac{\partial (u, v)}{\partial (x, y)} \right| =\begin{vmatrix} u_{x} & v_{x} \\ u_{y} & v_{y} \end{vmatrix}$ is the Jacobian determinant. $|J|$ is the absolute value.

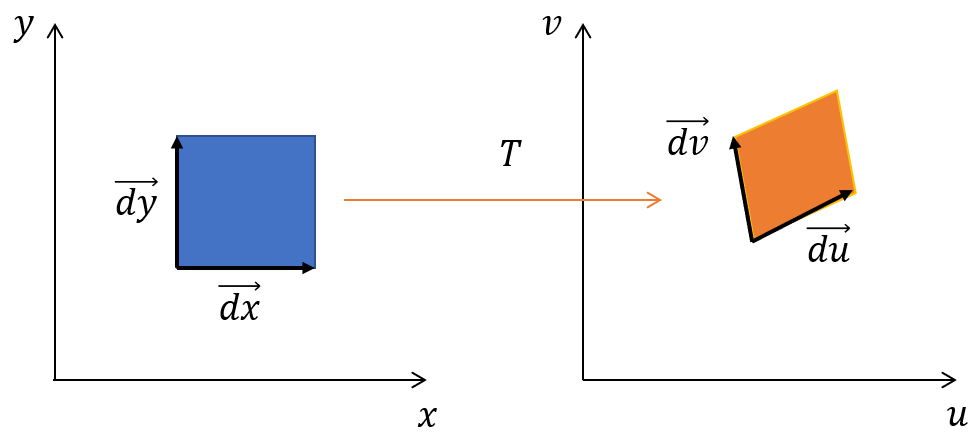
Figure 2: Schematic drawing of area transformation.

2 Liouville’s theorem

Let us start with two examples.

Example 1. Consider a free particle with mass $m$ moving in constant velocity $v$ in one dimension. It can be described by its position $q$ and momenta $p$ . Its time dependent trajectory in phase space $\Gamma = (q, p)$ follows the Hamilton’s equations

$\begin{equation} \dot{p} = -\frac{\partial H}{\partial q} = 0 \label{eq:p} \end{equation}$

$\begin{equation} \dot{q} = \frac{\partial H}{\partial p} = \frac{p}{m} \label{eq:q} \end{equation}$

where the Hamiltonian is . The time evolution of the trajectory from to is given by the solution to the equations ( $\ref{eq:p}$ ) and ( $\ref{eq:q}$ ):

$\begin{equation} p' = p \label{eq:ps} \end{equation}$

$\begin{equation} q' = q + \frac{p}{m} (t' - t) \label{eq:qs} \end{equation}$

Therefore the Jacobian determinant of the transformation from $(q, p)$ to $(q', p')$ is

$J(t, t') = \frac{\partial(q', p')}{\partial(q,p)} = \begin{vmatrix} 1 & \frac{t' - t}{m} \\ 0 & 1 \end{vmatrix} = 1$

Equation ( $\ref{eq:new.area}$ ) yields $dp'dq'=dpdq$ .

Example 2. Consider a particle of mass $m$ subject to a linear restoring force $F = -kx$ , corresponding to the quadratic potential

$\begin{equation} V(x) = \frac{1}{2} k x^2 = \frac{1}{2} m \omega^2 x^2 \label{eq:V} \end{equation}$

where $\omega = \sqrt{k/m}$ . In the Hamiltonian description of classical mechanics, the system is described by the dynamical variables $(x, p)$ , and the evolution is governed by the Hamilton’s equations of motion

$\begin{equation} \dot{x} = \frac{\partial H}{\partial p} = \frac{p}{m} \label{eq:xho} \end{equation}$

$\begin{equation} \dot{p} = -\frac{\partial H}{\partial x} = -m \omega^2 x \label{eq:pho} \end{equation}$

where $H$ is the Hamiltonian:

$\begin{equation} H = T + V = \frac{p^2}{2m} + \frac{1}{2} m \omega^2 x^2 \label{eq:Hho} \end{equation}$

Upon taking a second derivative, equations ( $\ref{eq:xho}$ ) and ( $\ref{eq:pho}$ ) become

$\begin{equation} \ddot{x} + \omega^2 x = 0 \;\;\;\;\;\; \ddot{p} + \omega^2 p = 0 \label{eq:wave} \end{equation}$

The general solutions to equations ( $\ref{eq:wave}$ ) are

$\begin{equation} x(t) = A \sin (\omega t + \delta) \label{eq:solx} \end{equation}$

$\begin{equation} p(t) = A m \omega \cos (\omega t + \delta) \label{eq:solp} \end{equation}$

The microstate of the system at some other time can be written down from equations ( $\ref{eq:solx}$ ) and ( $\ref{eq:solp}$ ) as

$\begin{equation} x(t') = \frac{1}{m\omega}\sin(\omega (t' -t)) p(t) + \cos(\omega (t' -t)) x(t) \label{eq:tx} \end{equation}$

$\begin{equation} p(t') = \cos(\omega (t' -t)) p(t) - m \omega \sin(\omega (t' -t)) x(t) \label{eq:tp} \end{equation}$

The Jacobian determinant of the transformation defined by equations ( $\ref{eq:tx}$ ) and ( $\ref{eq:tp}$ ) is

$J(t, t') = \frac{\partial(q', p')}{\partial(q,p)} = \begin{vmatrix} \cos(\omega (t' -t)) & \frac{1}{m\omega}\sin(\omega (t' -t)) \\ m\omega\sin(\omega (t' -t)) & -\cos(\omega (t' -t)) \end{vmatrix} = -1$

So we have again $dx'dp'=dxdp$ .

In general, let us consider a system consisting of $N$ particles in 3 dimensions. At any time $t$ , each particle $j$ is described by its position vector $\overrightarrow{q_j} = (q_{j,x}, q_{j,y}, q_{j,z})$ and momenta vector $\overrightarrow{p_j} = (p_{j,x}, p_{j,y}, p_{j,z})$ . Thus the whole system at any time is described by a $6N$ dimensional vector $\overrightarrow{X} = (\overrightarrow{q_1}, \overrightarrow{p_1}; \overrightarrow{q_2}, \overrightarrow{p_2}; \cdots, \overrightarrow{q_N}, \overrightarrow{p_N};)$ in a $6N$ dimensional phase space. If the transformation from time $t$ to another time $t'$ is defined by the Hamilton’s equations of motion

$\begin{equation} \begin{split} \dot{q}_{j, \alpha} & = \frac{\partial H}{\partial p_{j, \alpha}} \\ \dot{p}_{j, \alpha} & = -\frac{\partial H}{\partial q_{j, \alpha}}, \; \alpha = x, y, z, \end{split} \end{equation}$

then the absolute value of Jacobian determinant of the transformation is 1. This is the Liouville’s theorem.

Proof. According to equation ( $\ref{eq:new.area}$ ), it is enough to prove the volume of the region

$\Delta X = \{\overrightarrow{X}\mid \overrightarrow{q_1} \in \Delta q_1, \overrightarrow{p_1} \in \Delta p_1; \cdots; \overrightarrow{q_N} \in \Delta q_N, \overrightarrow{p_N} \in \Delta p_N\}$

is a constant with respect to $t$ .

Using Taylor expansion, we obtain that

$\begin{equation} \begin{split} \Delta q_{j, \alpha}(t+\delta t) & \approx \Delta q_{j, \alpha}(t) + \delta t \Delta \dot{q}_{j, \alpha}(t) \\ & = \Delta q_{j, \alpha}(t) \left(1 + \delta t \frac{\Delta \dot{q}_{j, \alpha}(t)}{\Delta q_{j, \alpha}(t)}\right) \end{split} \label{eq:Deltaq} \end{equation}$

$\begin{equation} \begin{split} \Delta p_{j, \alpha}(t+\delta t) & \approx \Delta p_{j, \alpha}(t) + \delta t \Delta \dot{p}_{j, \alpha}(t) \\ & = \Delta p_{j, \alpha}(t) \left(1 + \delta t \frac{\Delta \dot{p}_{j, \alpha}(t)}{\Delta p_{j, \alpha}(t)}\right) \end{split} \label{eq:Deltap} \end{equation}$

The volume of $\Delta X$ is

$\begin{equation} \begin{split} \left|\Delta X(t + \delta t)\right| & = \Pi_j \Pi_{\alpha} (\Delta q_{j, \alpha}(t+\delta t) \Delta p_{j, \alpha}(t+\delta t)) \\ & \approx \left|\Delta X(t)\right| \left[ 1 + \delta t \sum_j \sum_{\alpha} \left(\frac{\Delta \dot{q}_{j, \alpha}(t)}{\Delta q_{j, \alpha}(t)} + \frac{\Delta \dot{p}_{j, \alpha}(t)}{\Delta p_{j, \alpha}(t)} \right) \right] \end{split} \end{equation}$

Therefore,

$\begin{equation} \begin{split} \frac{d}{dt}\left|\Delta X(t)\right| &= \lim_{\delta t \rightarrow 0} \frac{\left|\Delta X(t + \delta t)\right|-\left|\Delta X(t)\right|}{\delta t} \\ & = \left|\Delta X(t)\right| \sum_j \sum_{\alpha} \left(\frac{\partial \dot{q}_{j, \alpha}(t)}{\partial q_{j, \alpha}(t)} + \frac{\partial \dot{p}_{j, \alpha}(t)}{\partial p_{j, \alpha}(t)} \right) \\ & = \left|\Delta X(t)\right| \sum_j \sum_{\alpha} \left(\frac{\partial}{\partial q_{j, \alpha}(t)} \frac{\partial H}{\partial p_{j, \alpha}} - \frac{\partial }{\partial p_{j, \alpha}(t)}\frac{\partial H}{\partial q_{j, \alpha}} \right) \\ & = 0 \end{split} \end{equation}$

This implies that $\left|\Delta X(t)\right|$ is a constant. Thus the absolute value of the Jacobian determinant is 1.

3 Jarzynski equality

Assume the equilibrium state inside the test tube is changed with time from its initial state $A$ to final state $B$ along some path $\gamma$ because external work $W$ is done on the test tube system. The work $W$ depend on the initial and final microscopic conditions of the system. Since the initial state of the system is a random variable, the work is a random variable. Jarzynski has proved that the average of the Boltzmann weight of the work is related to the Helmholtz free energy by the following equality (Jarzynski 1997)

$\begin{equation} \overline{\exp\left(-\beta W\right)} = \exp\left(-\beta \Delta F\right) \label{eq:JE} \end{equation}$

where $\beta \equiv 1/k_BT$ . This equality tells us that the Helmholtz free energy (equilibrium information) can be extracted from the ensemble average of the Boltmann weighted work performed on the system to change the system equilibrium state from $A$ to $B$ . The result is independent of both the path $\gamma$ from $A$ to $B$ , and the rate at which the system is changed along the path.

For simplicity, we assume that the system’s trajectory from state $A$ to state $B$ along a path $\gamma$ can be characterized by a time-dependent parameter $\lambda(t)$ , $0 \le t \leq \tau$ . Let denote a point in the phase space of the system, and let the Hamiltonian for the system, parameterized by . Let us prove equality ( $\ref{eq:JE}$ ).

Proof. The work done on the system along the path $\gamma$ from state $A$ to state $B$ is

$\begin{equation} \begin{split} W(\boldsymbol{z}(0), \boldsymbol{z}(\tau)) & = \int_{0}^{\tau} \frac{\partial H(\boldsymbol{z}, \lambda)}{\partial \lambda} \frac{d\lambda}{dt}dt \\ & = \int_{0}^{\tau} \frac{d H(\boldsymbol{z}(t), \lambda(t))}{dt} dt \\ & = H(\boldsymbol{z}(\tau), B) - H(\boldsymbol{z}(0), A) \end{split} \label{eq:jarzW} \end{equation}$

Let $Z_{A}$ and $Z_{B}$ be the partition function for state $A$ and state $B$ , and $F_{A}=-\beta^{-1}\ln Z_{A}$ and $F_{B}=-\beta^{-1}\ln Z_{B}$ be the free energy. Since $\boldsymbol{z}_0 \equiv \boldsymbol{z}(0)$ is a random variable, $\boldsymbol{z}_{\tau} \equiv \boldsymbol{z}(\tau)$ is also a random variable.

$\begin{equation} \begin{split} <e^{-\beta W}> &= \int d\boldsymbol{z}_0 \frac{1}{Z_{A}}e^{-\beta H(\boldsymbol{z}_0, A)} e^{-\beta W(\boldsymbol{z}_0)} \\ & = \frac{1}{Z_{A}}\int d\boldsymbol{z}_0 e^{-\beta H(\boldsymbol{z}_{\tau}, B)} \\ & = \frac{1}{Z_{A}}\int d\boldsymbol{z}_{\tau}\left|\frac{\partial \boldsymbol{z}_{\tau}}{\partial \boldsymbol{z}_{0}}\right|^{-1} e^{-\beta H(\boldsymbol{z}_{\tau}, B)} \\ & = \frac{Z_{B}}{Z_{A}} \\ & = e^{-\beta \Delta F} \end{split} \label{eq:proofJE} \end{equation}$

where $\left|\frac{\partial \boldsymbol{z}_{\tau}}{\partial \boldsymbol{z}_{0}}\right|=1$ is due to the Liouville’s theorem.

Proposition 3.1 $\left<W\right> \geq \Delta F$ , which is the inequality of Clausius.

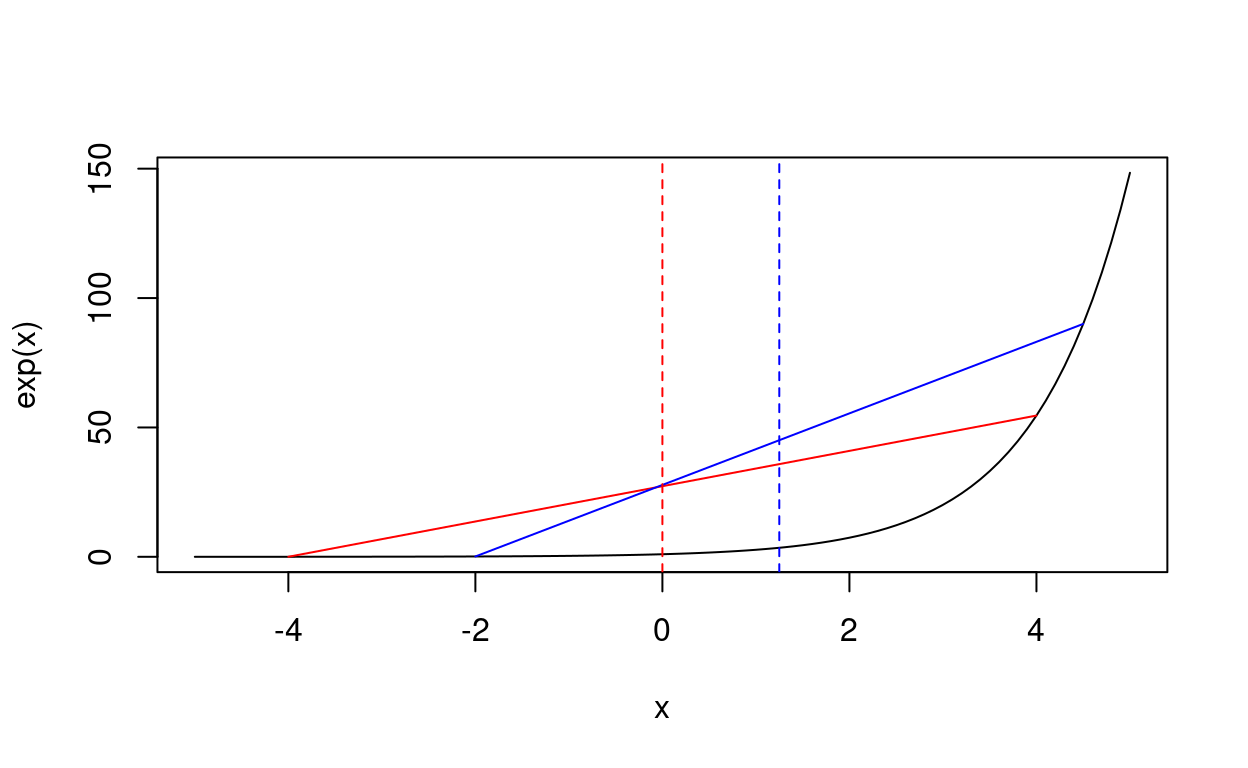
Figure 3: Exponential function is concavity.

Since exponential function is a concavity function, any secant line lies above the curve as shown in Figure 3. Therefore , which is called the Jensen’s inequality. Applying the Jensen’s inequality to equality ( $\ref{eq:JE}$ ), we obtain that $\left<W\right> \geq \Delta F$ .

References

Jarzynski, C. 1997. “Nonequilibrium Equality for Free Energy Differences.” Phys. Rev. Lett. 78 (14): 2690–3. https://doi.org/10.1103/PhysRevLett.78.2690.